
Underpinning the coherence of statistical process control, process capability analysis and numerous other statistical applications is a phenomenon found throughout nature, the social sciences, athletics, academics and more. That is, the normal distribution, or less formally, the bell curve. Because of its ubiquity, this normal distribution is arguably the most important data model analysts, engineers, or quality professionals will learn.
The normal distribution is a type of frequency distribution characterized by its bell shape—that is, symmetrical about its average value with a decreasing probability of occurrence at its extreme values. Consider for a moment Figures 10 and 11. Both roughly display this bell shape, yet the sources of their data are vastly different.
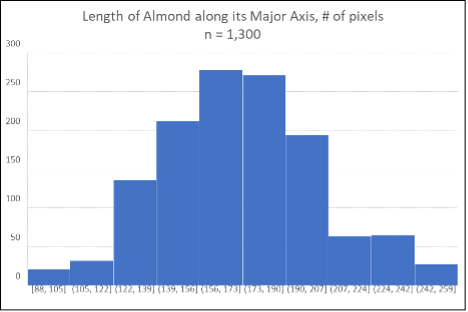
Figure 10 is a histogram showing the frequency distribution of the weights of professional National Basketball Association players during the 2023-2024 season. This data may useful to professional coaches, aspiring players, athletic trainers, recruiters, and sports enthusiasts. The histogram in Figure 11 displays the distribution of the lengths of a 1,300-piece sample of randomly selected California almonds, as measured by a machine vision system and image processing software. This analysis is useful to a mere handful of agronomists and automated nut-cracking machine design engineers.
So how can the histograms of these very different populations look so similar? The answer is rooted in a statistical law called the Central Limit Theorem, which states that when you take a large number of independent events or data points and combine them, their average will tend to form a normal distribution, regardless of the original distribution of the individual events.
Imagine you’re building a mountain of sand by dropping thousands of tiny grains from above. Each grain might fall in a slightly different spot, but as you keep dropping more grains, the shape of the mountain starts to look the same every time—rounded and symmetrical, with most of the sand piling up in the middle and tapering off evenly on both sides.
This is similar to how the normal distribution works. Even if the individual events (like the path of a grain of sand) are different and somewhat random, when you look at the big picture, the combined result tends to form a bell-shaped curve.
The normal distribution shows up in many different situations because many processes are the result of adding up small, independent factors. Whether it’s the height of people, the length of almonds, or the variation in a manufacturing process, these are all influenced by multiple small, random effects. When these effects are combined, the outcome is often a normal distribution.
So, even though the events themselves might be different, the way they combine leads to that familiar bell curve, making the normal distribution a common pattern in the natural world and in human-made processes.
Ray Harkins is the General Manager of Lexington Technologies in Lexington, North Carolina. He earned his Master of Science from Rochester Institute of Technology and his Master of Business Administration from Youngstown State University. He also teaches manufacturing and business-related skills such as Quality Engineering Statistics, Reliability Engineering Statistics, Failure Modes and Effects Analysis (FMEA), and Root Cause Analysis and the 8D Corrective Action Process through the online learning platform, Udemy. He can be reached via LinkedIn at linkedin.com/in/ray-harkins or by email at the.mfg.acad@gmail.com.

Leave a Reply