Sample Size – Measuring a Continuous Variable
Introduction
When planning a test on a continuous variable, the most common question was “How many should I test”? Later, when the test results were available, the questions were “What is the confidence?” or “How precise was the result?” This article focuses on planning the measurements of a continuous variable and analyzing the test results.
Definition
A continuous variable is a variable that has an infinite number of possible values. This contrasts with a discrete variable which can take on a finite number of values. Examples of continuous variables would be dimensions, weight, electrical parameters, plus many others.
The Data
Let’s assume we want to determine the value for a characteristic. There are parts available to measure so we take one measurement per part. The measurements are close, but don’t agree.
If the data is plotted in a frequency histogram, generally there is a pattern that shows a center and variation about the center. Usually the data exhibits the bell curve indicative of a normal distribution. Since the center appears is a common value, but the center value changes with each sample of parts. We need a simple statement of the value of the center, some measure of the measurement accuracy, and some confidence in the results.
The Central Limit Theorem
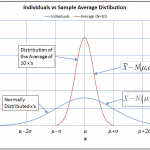
In another article, I discussed “The Central Limit Theorem”, which states that the data average is approximately normally distributed even if the data distribution is non-normal. A comparison of normally distributed x’s and the distribution of averages of 10 x’s is shown graphically, figure 1.

Figure 1
Note, that the distribution of the average is much narrower than the distribution of the individuals. When X is normally distributed about a mean μ with standard deviation σ, a short hand notation used by statisticians is $-X\sim N(\mu,\sigma^2)-$. Here N indicates the normal distribution, not sample size. Then, the distribution of the averages of size n is $-\bar{X}\sim N(\mu,\sigma^2/n)-$.
The sample statistics and S provide estimates of the population parameters μ and σ, where
$$\bar{X}=\frac{1}{n}\sum_{i=1}^{i=n}X_i$$
(1)
and
$$S^2=\frac{1}{n-1}\sum{(X_i-\bar{X})^2}$$
(2)
The Math
Both $-\bar{X}-$ and S are subject to sampling variation. We don’t know the distribution of $-\bar{X}-$ about μ because we don’t know μ and σ. In my article “Estimating Normal Distribution Parameters and Tolerance Limits”, it was shown that the distribution of μ values follow a t-distribution. The appropriate probability statement is
$$Pr(\bar{X}+t_{\alpha/2,n-1}<\mu<\bar{X}+t_{1-\alpha/2,n-1})=1-\alpha$$
(3)
The tolerance interval is on μ is $-(\bar{X}+t_{\alpha/2,n-1},\bar{X}+t_{1-\alpha/2,n-1})-$. This interval looks odd, but it is a consequence of the fact that when α<0.5, the values of t are negative.
A tolerance is desired to contain $-\mu-$ within $-\pm\Delta-$ of $-\bar{X}-$, expressed as
$$\bar{X}\pm\Delta$$
(4)
When C is specified, then the appropriate significance level is $-\alpha=1-C-$. The tolerance Δ is determined using equation 3.
$$\Delta=t_{1-\alpha/2,n-1}S/\sqrt{n}=-t_{\alpha/2,n-1}S/\sqrt{n}$$
(5)
From equation 5, Δ is proportional to S, decreases with increasing sample size, and increases if higher confidence is desired. Equation 5 can be rearranged to form the equation 6.
$$n=(t_{\alpha/2,n-1}S/\Delta)^2$$
(6)
Equation 6 is a difficult to solve since n occurs in both sides of the equation. The calculation may require an iterative process to determine the best possible value. When test sample sizes are large, the value of the $-t_{\alpha/2,n-1}-$ statistic approaches the $-z_{\alpha/2,n-1}-$ statistic, so some analysts use equation 7.
$$n=(z_{\alpha/2}S/\Delta)^2$$
(7)
Equation 7 has the advantage of the simplicity of using z-value from a normal distribution table. The problem is that the t-value diverges from the z-value at small sample sizes. A reasonable approach is to use equation 7, to obtain an approximate sample size. Then iteratively use equation 6 to obtain a precise sample size.
Test Planning
When planning a test, the sample size required to contain μ in interval $-\bar{X}\pm\Delta-$ with C confidence needs to be calculated. Δ is to be half the size of a standard deviation, so S/Δ=2. Then C=0.9, α=0.1, and α/2=0.05. The preliminary calculation is made to estimate n using zα/2=-1.645, yielding
$$n=(-1.645*2)^2=10.8$$
which is rounded up to 11 samples. The next step is to improve the calculation using the more accurate t-value. The sample size of 11 provides t0.05,10=-1.812, yielding
$$n=(-1.812*2)^2=12.13$$
which is rounded up to 13 samples. Iteratively, we repeat the t calculation again with n=13, t0.05,12=-1.796, so now
$$n=(-1.796*2)^2=12.85$$
which again is rounded to 13 samples. The final test plan would specify 13 samples.
Test Analysis
Once the test was completed and the measurements analyzed, an analysis should confirm the original test planning assumptions. For example, the standard deviation was assumed, but the sample standard deviation S, may be different. The confidence should be recalculated. By rearranging equation 6,
$$t_{\alpha/2,n-1}=\frac{\Delta\sqrt{n}}{S}$$
(8)
A convenient way to solve equation 8 for the confidence is to use the Excel function,
$$C=1-2*tdist(\Delta\sqrt{n}/S,n-1,1)$$
(9)
Or
$$C=1-tdist(\Delta\sqrt{n}/S,n-1,2)$$
(10)
Example
Suppose the test results are analyzed and Δ=0.5, the sample standard deviation is S=0.8, and n=13, what is the confidence C? Using the excel function in equation 10, C=95.6%
Conclusion
Test sample sizes can be calculated when
- The precision Δ of the interval that contains μ is specified.
- Some preliminary estimate of the sample standard deviation S is available.
- The confidence C is specified.
The calculation procedure is
- Calculate a preliminary sample size using $-n=(z_{\alpha/2}S/\Delta)^2-$. $$ound n up to the next higher integer.
- Calculate sample sizes using $-n=(t_{\alpha/2,n-1}S/\Delta)^2-$ starting with the previous estimate. R0und n up to the next higher integer.
- Repeat step 2 until n does not change.
Test planning should be followed up with an analysis using the actual test results.
Note
If you want to engage me on this or other topics, please contact me. I offer a free hour for the first contact to discuss your problem/concerns and to determine how I can help you.
I have worked in Quality, Reliability, Applied Statistics, and Data Analytics over 30 years in design engineering and manufacturing. In the university, I taught at the graduate level. I also provide Minitab seminars to corporate clients, write articles, and have presented and written papers at SAE, ISSAT, and ASQ. I want to help solve your design and manufacturing problems.
Dennis Craggs, Consultant
810-964-1529
dlcraggs@me.com
This topic was something which I was not able to understand it easily. After going through your article it became very easy for me to understand it. Now I am well prepared for my exams. Thanks for the detailed information.
I am glad the article was helpful. Sometimes the instruction of difficult topics leaves something to be desired. I found that teaching with a combination of tools works best, i.e., graphics, mathematics, and a good verbal description. Thanks for the feedback.
Thank you sir how can Calculate sample size for my thesis which have continuous outcome variable
Hi Alemker, this article has a few clues and of course the appropriate method depends on what you are seeking to learn and how well. cheers, Fred
Hi Alemker, an appropriate sample size depends on the type of data being analyzed. This article assumes the population is continuous, one-dimensional, and normally distributed with a constant mean and standard deviation. If the mean or standard deviation changes, then you are measuring an unstable process. If you are measuring something that is variable, then the residual (=actual-measured) may be your random variable. Other situations, like measuring location in 3-dimension don’t fit the model. If you provide more details and I will try to assist you. Dennis
Hi Dennis,
Can you point me to a reference where I can read about computing minimum sample size for data containing:
1. multiple continuous variables (in my case, ten, all having values in range 0 to 1)
2. one binary variable
3. one integer valued variable (most values lying in the range 1-25, but can go up to 70)
Regards,
Tarun
1) For multiple continuous variables, is there a value that is critical?
If the stack is linear, then the critical value is a combination of the component values. Use a Tolerance Stack Analysis to estimate the critical mean from the individual variable means. Also, the variance in the critical result will be the sum of the individual variance. Lots of statistics texts and articles on the internet discuss this.
If non-linear, the problem is tougher. Consider the geometry of a suspension system which includes individual parts. There probably is a measurement that is the result of joining these parts together, like the caster or camber of the wheels. The individual part dimensions can be combined in a simulation and assembly measurement calculated. This process, repeated many times is a Monte Carlo simulation. The tolerance of the assembly measurement is the topic of Variation Simulation Analysis.
2) For a binary variable, the probability of one outcome is p and the probability of the other is $-q=1-p-$. The variation in p should follow a binomial distribution. With enough samples, the variation in P can be approximated with a normal distribution, if $-np\geq0-$. Again, we don’t know p before collecting data. A good reference is “Quality Control and Industrial Statistics” by Acheson J Duncan.
3) I suggest you look at the histogram of your integer valued variable. Does it approximately follow a known distribution? Since you indicated the data was skewed, consider using a lognormal or Weibull probability plot of the data for the assessment. If it follows a lognormal distribution, then the log of the variable will be normally distributed. At that point, consider apply sample size calculations to the log of your variable.
Hello Dennis,
Could you explain what you meant by “Δ is to be half the size of a standard deviation, so S/Δ=2.” Is this an assumption?
Thank you.
There are 4 variables in the relationship, i.e., sample size n, the tolerance $-\Delta-$, the sample standard deviation S (unknown), and the significance $-\alpha-$. To plan the test, consider the geometry of the problem. The variation of the average will be less than the variation of the population. A more precise is obtained by adjusting the sample size. Higher sample size provide a more precise estimates of the mean. So how precise? I set a goal of knowing the tolerance to half the value of the sample standard deviation, i.e., S/$-\Delta-$=2. You can say it is arbitrary, but test planning involves multiple variables to design cost effective tests. You could say selecting a confidence of 95% is arbitrary. If a test is very expensive to run, you reduce the confidence level and desired tolerance. It’s all a tradeoff.