
Introduction
Sometimes, non reliability practitioners assume that a Reliability Analysis is just about “tossing” a distribution at a set of data. It is a little bit more complex than this. There needs to be some sort of engineering validation on the final outcome. The question to be asked is: “does this life model used make engineering sense?” This article highlights the importance of choosing the correct statistical distribution. The alternative leads to flawed decision making and can be detrimental especially when dealing with critical equipment or million-dollar decisions. A worked example is also provided.
What is Reliability Analysis?
Reliability Analysis or Life Analysis uses statistical tools to define life characteristics of assets or components. Using historical records such as operating time, one can define characteristics of equipment informing an operator of the future number of failures or probabilities of failures. And other useful information that will contribute to preserving asset health.
The key input to reliability analysis is asset performance records, typically obtained through maintenance records. The repository for those records is typically the Computer Maintenance Management System (CMMS). As disserted by Larry George, other records can also be used towards the analysis, in the absence of a CMMS repository1.
2 Parameter versus 3 Parameter Weibull Distributions
The Weibull Distribution is a very popular distribution in Reliability Engineering. Sometimes a little too popular. As it tends to be misused or literally abused. There are typically 2 types of Weibull Distributions based on their number of parameters, i.e. 2 Parameter and 3 Parameter Weibull Distributions. The number and value of each parameter in the distribution will influence the life characteristics of the asset studied. Described below are the two distribution types.
- 2 Parameter Weibull is the most common Weibull Distribution with a Shape Parameter Beta (β) and a Scale Parameter Eta (η). The reliability function associated with this distribution is defined as follows.
- The 3 Parameter Weibull Distribution has an extra parameter, Gamma (γ).
Gamma is the failure free interval. A failure free interval in the 3P Weibull Distribution implies that during an initial interval, the probability of failure is nil. The typical example is a consumable sitting in storage before being put in service. Whilst it is in storage, it is not subject to any destructive stresses. A Roller Bearing or Gasket fit this category. Obviously, one assumes that the storage conditions are adequate. For example, there is no corrosion degradation or mishandling damage.
Analytical Example
Below is an example of Life Analysis estimation for a population of Roller Bearings. I have provided the raw data with this link should you want to reproduce the calculations. The best life model fit defaults to a 3 Parameter Weibull Distribution as shown in Graph 1 below.
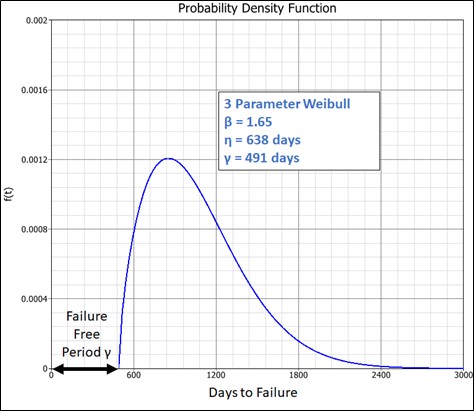
The Shape Parameter Beta is 1.65. Beta is greater than 1. Implying that after being put in service, the bearing’s failure rate will increase with time. Using this information, a plan can be implemented to replace the bearing at the most economical time. That is identifying the most effective maintenance strategy.
The Scale Parameter Eta is 638 days. Also known as the bearing Characteristic Life. It gives the analyst an idea of when we can expect the first failure. Additionally, the probability of failure of the bearing at time equal to Eta is 63.2%. And Reliability at time Eta is:
R(η)=36.8%
The new parameter is the failure free period Gamma equal to 491 days. Graph 1 above illustrates the value of Gamma. Note the graphical offset from time zero to 491 days. This implies that the bearing is not in service before approximately 500 days.
Using the same data set, we impose a 2 Parameter Weibull Distribution on it. Graph 2 below illustrates both 2 and 3 parameter Weibull models.
When a Life Analysis Model is established, a test is performed to evaluate how well the chosen distribution or analysis method fits the data set. In Table 1 below, we have the results of the evaluation for both distributions.
The Rho or Correlation Coefficient is a measure of how well the regression line falls onto a straight line on a probability plot. In the above case the 3 Parameter Weibull model shows the least scatter hence a better model.
The LK or Likelihood Function value compares how well different models fit the same data set. The model with the highest LK value is considered to provide the best statistical fit. And this also applies to the 3 Parameter Weibull since its LK value is closer to zero.
However, one must be most careful that the model chosen makes engineering sense. I have witnessed evaluations showing best fits that do not makes sense from a reality standpoint. In the above example, a 3 Parameter Weibull model makes sense. A failure free period is consistent with bearing storage.
The CMMS records in our case, starts recording the bearing life as soon as it is put in storage. This is the reason why we have a failure free period. This could also apply to a domestic kettle being sold in a shop. If records start when the kettle is placed on the shop shelf or from the time it is manufactured, there would be a failure free period until the time its is put in service in someone’s kitchen. However, if the life records starts when the bearing or kettle went into service (i.e., installed in equipment or boiled the first batch of water), then a failure free period would not be justified. One would expect a 2 Parameter Weibull to fit the data. In other words, a 2 Parameter Weibull would make engineering sense.
In summary, it is important to pause after any engineering calculations and evaluate the final results. One of my mentors had a saying back then; “Engineers who work alone make mistakes. Engineers who work in teams avoid them”. So, in essence, always get your peers to review your results if possible. And always ask the reviewer and yourself: “Do those results make engineering sense?”
References
1 – Larry George, 2024, Do the Best You Can With Available Data?, Accendo Reliability.


Leave a Reply