My first task at Apple Computer was to recommend the warranty duration for the Apple II computer. Apple didn’t have a warranty! So, I looked at competitors’ warranties and recommended the same, one year. I wish I had known Apple’s computers’ and service parts’ reliabilities before that recommendation; I would have used actuarial forecasts of warranty returns to compare alternative warranties. Apple’s hardware warranty is still one year. Is that equitable to Apple, its customers, and society?

I am not a lawyer, and I don’t plan to sue anyone for negligence. However, there are consequences to oversimplified, uncertain, imperfect, and misleading reliability and risk practices. Field reliability statistics quantify and describes what really happens. Field reliability statistics are fundamental to reliability related decisions about: 

• warranty reserves and duration
• safety as in precautionary principles about uncertainty
• risk equity for producers AND consumers
• disclosure of reliability-related ESG measures: sustainability, resilience, and reliability?
• actions on regulations, requirements, standards, and certifications. 

Federal regulations and military standards have reliability-related advice and guidelines. ISO standards 9000 (design and development, software), 14001 (environmental management), 14224 (data exchange), 26000 (social responsibility), and 31000 (risk management) have some guidance. Regulations and standards preserve tradition, avoid change, and support consultants, software vendors, and professional organizations. What could field reliability do to advance knowledge and support consumers?

Some people believe “disclosure of age-specific field reliability should improve market share.” Geoffrey Randolph gave me the chance to demonstrate. He shared Uniphase laser ships and returns counts. I compared nonparametric field reliability estimates of Uniphase laser population with Abbott Diagnostics Division’s (ADD) Uniphase lasers. (This required deconvolving sell-through time from time to failure distribution. The ADD laser purchaser was hoarding new lasers in a closet.) Uniphase published an advertisement showing an old man running around a stadium track. (Was that old runner Charles Townes, one of the inventors of lasers, running around the UC Berkeley stadium?) The advertisement also showed the nonparametric, age-specific field reliability of the Uniphase laser. Uniphase failed to forecast sales in 2001 and risked legal problems. An employee threatened a lawsuit claiming Uniphase couldn’t estimate reliability without life data! Uniphase is gone, but their lasers aren’t.

Reliability-related decisions are part of multi-objective, risk-based, organizational decision making. They should be based on available field reliability information, not just handbook MTBF predictions, material physics, lab tests, or subjective opinions. This article describes some reliability-related decisions and how field reliability information could help risk-based decision-making.

Warranty Reserves?

Somebody said, “If you make an actuarial forecast of warranty returns, warranty reserves can be expensed. Insurance companies make actuarial forecasts. That’s why Warren Buffet bought GEICO.” Buffet could subtract warranty reserves from revenue without waiting for actual warranty returns. (He could avoid tax if warranty costs were less than warranty reserve expense!). Actuarial (age-specific) warranty returns forecasts depend on field reliability warranty duration and conditions. The actuarial returns forecast is ∑d(t-s)*n(s), s=1,2,…,warranty, where n(s) is the installed base of age s under warranty, and d(t-s) is the condition-dependent, age-specific return rate for installed base of age t-s. (d(t-s) is not always the same as actuarial failure rate a(t-s) at first failure!)

Warranty reserve calculation should include variance [or standard deviation] of warranty costs as well as forecast failures [Kulkarni et al.]. It should also include the warranty conditions on replacements, a renewal process [https://fred-schenkelberg-project.prev01.rmkr.net/renewal-process-estimation-without-life-data/]? Variance of warranty costs includes covariances of demand rate function estimates, because the variance of the actuarial returns forecast is ∑Var[d(t‑s)]*n(s)^2+∑∑Covar[d(t‑s),d(t)]*n(s)*n(t). I used the bootstrap for maximum likelihood variance-covariance estimates in table 1. 

Table 1. CD-ROM ships and returns counts, actuarial returns forecasts (E[Returns]), and their standard deviations (bootstrapped 10 times). Data are from May 1988 to Oct. 1993. Table 1 used first 36 months of data in maximum likelihood actuarial failure rate estimates. The maximum likelihood estimator blew up after 36 months, because ships were negative or less than returns. 

Month	Ships	Returns	E[Returns]	Standard deviation
1	551	2	1	0.66
2	620	0	1	1.88
3	689	9	7	2.40
4	758	9	8	4.36
5	827	9	8	4.46
6	896	12	10	101
7	965	12	11	97
8	1034	13	12	1109
9	264	26	56	1103
10	270	34	62	1097
11	288	53	60	1090
12	324	60	66	1082
Etc.

Capital markets see warranty reserves as reliability signals, and they price the firm’s stock accordingly. “Firms use warranty policies as a business strategy to promote their products” “We find that the stock market recognizes that warranty liabilities of firms that managed earnings are underestimated.” “A warranty is an effective means for reducing uncertainty about the product’s future performance…” [Cohen et al.], if the maker or vendor of the product knows its products’ field reliability.” According to the Financial Accounting Standards Board [https://www.FASB.org/home/], warranty expenses should be recognized when they are probable and can be estimated…While recording the event in the financial statements, the company will debit (charge) the warranty expense account and credit (accrue) a liability account when the product is sold to a client.” [CFI Team]

“Practitioners must carefully consider several tests under Sec. 461 to determine the deductibility of accrued warranty expense for tax purposes, paying particular attention to whether a fixed liability exists at the end of the year. The practitioner must analyze and document whether the all-events test has been met and economic performance has occurred before considering whether the recurring item exception applies to the accrued warranty liability.” [Kinkaid and Federanich] 

Precautionary Principles Include Reliability Uncertainty?

Precautionary principles deal with potential harm when knowledge is lacking. Field reliability knowledge is available for new products, because parts, customers, processes, usages, and environments are usually not new. That knowledge includes statistical uncertainty.

When there are threats of serious or irrevocable damage, lack of full scientific certainty shall not be used as a reason for postponing cost-effective measures to prevent environmental degradation. Quantify uncertainty as event probabilities times consequences [risk]. Quantify event probabilities as reliability or failure rate function estimates and their sample or population uncertainties. Quantify uncertainty with variance-covariance of reliability estimates.

Balakrishnan equitable: “it is important that an increase in efficiency is not achieved at the expense of an equitable allocation of resources.” [https://www.mit.edu/~hamsa/pubs/BalakrishnanChandranATM07.pdf]. This includes reliability-related allocation of resources; e.g., optimizing redundancy for resilience or designing products that stress cheap parts. I asked the chief engineer of a company why his vendors’ cheap parts in his products fared worse than the vendors’ parts in the vendors’ populations. He told me that’s because his company profits from service calls as well as their lower initial product purchase cost.

Risk Equity?

Social responsibility (ISO 26000) and Consumers’ Bills of Rights remind me that corporations might share product information. Consumers’ Bills of Rights include product information, which I interpret to include product field reliability. The Federal Trade Commission has rules about disposing of consumer-report information, which a company may collect regarding product complaints or failures.

I asked people for the age-specific field reliability of their companies’ products I wanted to buy. Didn’t get much. Some people confessed that they didn’t know the field reliability of their companies’ products. I offered to give them nonparametric estimates in return for periodic ships and returns counts. A few did, some seemed baffled, and some said they’d have to consult their lawyers. The few who did share got nonparametric estimates of their products’ field reliability and used that information for competitive advantage [Uniphase lasers]. 

For a bad example, Reynolds and Reynolds, www.reyrey.com, collects automotive warranty service records from car dealers by age and mileage as well as services and parts replaced. This data makes it easy to estimate dealer service and parts’ demand rates, under warranty. What does R&R do with their information? They sell it back to the dealers. After warranty expiration, dealers and car owners don’t have much information. 

Consumer associations do product quality tests, and the results are associated with consumer behavior [Rroshi and Weischselbaumer]. Consumer Reports publications give automotive relative-reliability rankings, but not reliability function estimates [https://advocacy.consumerreports.org/]. I offered them, but Consumer Reports prefer survey samples. PlugInAmerica’s owner-survey data led to Tesla Model S field reliability estimates https://fred-schenkelberg-project.prev01.rmkr.net/bivariate-reliability-estimates-from-survey-data/#more-457496/.

An actuarial forecast of warranty returns times cost per warranty return, cost*∑d(t-s)*n(s), s=1,2,…,warranty, is expected warranty cost, a quantitative risk measure. Expected value (or cost) analysis is called “economic risk analysis.” 

“Risk management is the art of using lessons from the past to mitigate misfortune and exploit future opportunities—in other words, the art of avoiding the stupid mistakes of yesterday while recognizing that nature can always create new ways for things to go wrong. True risk management is about much more than numbers; it is the art of using numbers and quantitative tools to manage risk. Risk is a central, maybe the central, component of managing a financial organization. But risk management has something of a split personality. Managing risk is as much the art of managing people, processes, and institutions as it is the science of measuring and quantifying risk” [Coleman]. Lessons from the past are incorporated in field reliability estimates and returns costs. 

Unfortunately, asymmetry of information leaves consumers uninformed about product reliability and economic risk. This could lead to moral hazard; e.g., a company could expose the public to more risk if it doesn’t bear the full cost of the consequences. [See also https://en.wikipedia.org/wiki/Adverse_selection/] Adverse selection means buyers and sellers have different information. Some might take advantage of better information, aka information arbitrage. Is that equitable? 

“Risk equity is an ex-ante concept corresponding to a preference for equalizing the probability of dying across agents“ [Bernard et al.]. Consider “dying” to be failure of a product, part, or process. The social impact of reliability becomes clearer if you consider customer risk for as well as producer risk. Customers could make more informed purchase choices with product field reliability information. The environment could benefit from more reliable production and refining processes and from less waste, trash, and junk. When will management and government take advantage of the ability to make actuarial forecasts and nonparametric estimates of field reliability, from data required by GAAP? 

There are several reliability-based risk equity alternatives:

• equate producer and consumer probabilities of failures
• equate expected costs, or 
• equate discounted expected costs.

Table 2. Reliability-risk-equity formulations per unit of product: F(t) is the cumulative distribution function 1-P[Life > t], u is useful life duration > w warranty duration. Cc and Cp are Consumer and Producer costs of product failures. If Cc = Cp, reliability equity means F(u)=2F(w).

Risk Model	Consumer	Producer	Result
P[Failure] in useful life u	F(u)-F(w) u = life	F(w) w = warranty	F(u) = 2F(w)
Costs	Cc	Cp < Cc, maybe  Cp << Cc	F(u)/F(w)= (Cp+Cc)/Cc maybe »1
Discount rate r	Cc*òS[a(t)e‑rt]f(t)dt	» Cp*F(w)	Computable

Producer risk is the expected warranty cost, the warranty cost of failure times the actuarial warranty failure forecast, (warranty cost)*∑[a(t-s)*n(s), s = 0,1,…,t), (t = warranty plus some slack for sell-through time and return time). (n(s) is the under-warranty installed base of age s.) Consumer risk is the expected cost, after warranty but before end of life or end of product support. Risks might be discounted for future costs over the product life cycle 
∫e^‑ru∑[a(t‑s)n(s; u)]du, where r is the discount rate and the integral is over the calendar-time life cycle from u = 0 to age t at warranty or end-of-life cycle if sooner than warranty. Life cycle runs in calendar time to end-of-product life-cycle (not necessarily end of product support), and t is product age-at-failure as long as failure occurs before end of product warranty [Kulkarni et al.]. Include the distribution of random N(s; u) under warranty at calendar time u; N(s; u) may be random because of sales as well as attrition or failures. 

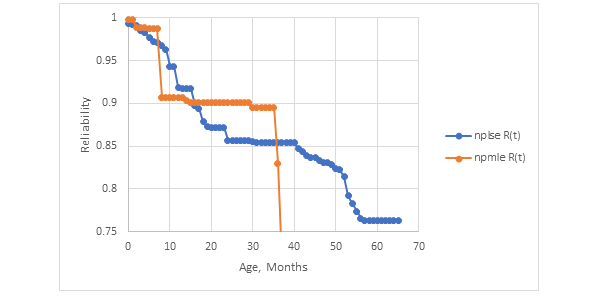
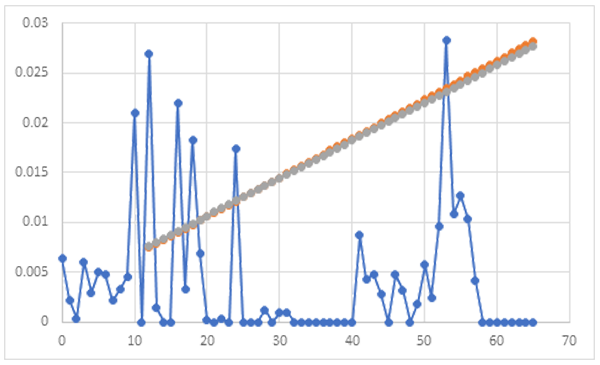
Naturally, actuarial failure rate functions have a bump around warranty, so continuous failure rate functions don’t fit: exponential, Weibull, gamma, etc. (figure 1). If you don’t use nonparametric statistics, fit a mixture distribution. You may use a continuous failure rate function rate function for extrapolation beyond age at warranty expiration to product end of life. 

Risk Equity is not same as reliability equity:

• P[Life < warranty] = P[Warranty < Life < End-of-Life] vs
• (Producer cost)*P[Life < warranty] = (Consumer cost)*P[Warranty < Life < EOL].

Suppose warranty duration was designed for risk equity? I.e., equate producer risk (expected cost of warranty returns plus extended warranties and recalls) with consumer risk (expected cost of failures after warranty expiration but perhaps before end-of-life support) [Runje et al.]?

For example, table 1 contains CD-ROM ships and returns. Nonparametric maximum likelihood and least squares gave the reliability and actuarial failure rate function estimates in figure 1.

I have asked companies for the age-specific field reliability of products I wanted to buy. I didn’t get much. Some people confessed that they didn’t know the field reliability of their companies’ products. I offered to give them nonparametric estimates if they would give me periodic ships and returns counts. A few did, some seemed baffled, and some said they’d have to consult their company lawyers. The few who did get nonparametric estimates of their products’ field reliability went on to use that information for a competitive advantage [Uniphase lasers]. I don’t know of any company that deliberately uses field reliability to set warranty duration; some companies use warranty reserves as a reliability signal [Cohen et al.]. Compared with disclosing the field reliability of products before and after warranty, warranty reserves are a weak signal.

I have asked companies for the age-specific field reliability of products I wanted to buy. I didn’t get much. Some people confessed that they didn’t know the field reliability of their companies’ products. I offered to give them nonparametric estimates if they would give me periodic ships and returns counts. A few did, some seemed baffled, and some said they’d have to consult their company lawyers. The few who did get nonparametric estimates of their products’ field reliability went on to use that information for a competitive advantage [Uniphase lasers]. Compared with disclosing the field reliability of products before and after warranty, warranty reserves are a weak signal.

I don’t know of any company that deliberately uses field reliability to set warranty duration. Assuming end-of-life is 60 months, table 3 shows the reliability equity warranty would have been 18 months to minimize the squared difference between P[Life <= warranty] and P[w<Life<EOL], using the reliability function estimated from CD-ROM ships and returns counts. 

Table 3. Warranty w to minimize SSE=(P[Life<=w]-P[w<Life<EOL])^2 = 0.00003 is 18 months

P[Life<=w]	0.0814	0.0827	0.0828	0.0828	0.1025	0.1055	0.1215	0.12757
P[w<Life<EOL]	0.1557	0.1545	0.1545	0.1545	0.1347	0.1317	0.1156	0.10966
SSE	0.0055	0.0051	0.0051	0.0051	0.0010	0.0007	.00003	0.00032
w, months	12	13	14	15	16	17	18	19

Table 4. Equitable risk warranty w is 13, 14 or 15 months to minimize SSE=
(ProducerCost*P[Life<=w]-ConsumerCost*P[w<Life<EOL])^2, where producer cost is $100 per return, and consumer cost is $150 per failure out of warranty but before end-of-life.

Producer $$$	8.15	8.28	8.28	8.28	10.25	10.55	12.16	12.76
Consumer $$$	23.36	0.15	0.15	0.15	0.13	0.13	0.12	0.11
SSE	231.6	65.94	65.94	65.94	102.35	108.54	144.98	159.92
w, months	12	13	14	15	16	17	18	19

You may discount risks during product life cycle, especially consumer risk, which occurs due to failures only after warranty expiration.

òEXP[-r*t]*(Producer cost|t)*P[Life <= warranty|t]dt = 
òEXP[-r*t]*(Consumer cost|t)*P[Warranty < Life < EOL|t]dt,

Integrate over calendar time t in the product life cycle plus warranty that extends beyond end-of-life support; end-of-life may not coincide with age of youngest products in the field! Setting warranty to equate consumer and producer risk also brings up the questions of how long will product be supported and what to do with in-warranty failures beyond end-of-life support. This is different from the warranty duration question, which is specific to product age since purchase, because product support may end at a calendar time regardless of the ages of products in the hands of consumers. End-of-life may occur due to company intentions, deliberate product obsolescence, or to external events. 5G networks made my wife’s Apple iPhone 5C obsolete last February. 

Regardless of end-of-life cause, risk equity requires reliability-related decisions on the part of the producer. Spare parts must be ordered and produced, stored, and then supplied when failures occur. 

Risk Equity Alternatives?

Different measures of equity depend on the participants. Brams et al. describe several equity measures and algorithms for maximizing group equity. “Utility” theory was developed to deal with differences [Keeney and Raiffa]. 

“The principal view I will advocate here is that risk equity concerns are almost invariably harmful to public welfare” [Viscusi]. That author cites cases where risk equity is NOT used fairly for public benefit. Viscusi proposes equity to be judged, not based on risk but based on equitable marginal costs of reducing risks. 

Risk equity may equate producer and consumer risk, but does that maximize public benefit? Ralph Keeney shows that risk equity could increase the probability of catastrophes. He published an article observing the increasing risk equity increased catastrophic death risk [Keeney]. Any utility function over the number of fatalities which exhibits risk equity must be risk prone. He has a specific meaning for risk prone (opposite of risk averse) in terms of utility functions. A person behaves as risk prone if the person prefers a lottery over certain receipt of the lottery’s expected value.  

Company decisions include product reliability as part of a multi-objective decision process, whether explicit or not [Keeney and Raiffa]. Their book is about risk and utility; it barely touches on equity in the last chapter. 

I worked as a teaching assistant for John Harsanyi (1994 Nobel prize in economic sciences, for game theory). Professor Harsanyi had a solution to the problem of decision maker utility as a function of factor vector X; u(X) (decision maker) = f(u1(X), u2(X),…, un(X, Reliability)) (n stake-holders’ utility functions), including the reliability stake holders [Harsanyi, Adler]. Harsanyi proposed joint stake-holder personal positions A and B and preferences, [X(A), Pa] and [X(B), Pb]. 

For example, I helped Cessna verify that their aircraft engine reliability under warranty was far less than promised. Lycoming made the engines. Lycoming owns Cessna. I wonder what the Cessna people told Lycoming and what Lycoming did consequently? 

Utility, regardless of whose utility it is, involves risk, and risk is expected value of cost, a function of reliability and its uncertainty. 

Social Responsibility (SR), ESG, and Risk vs. Uncertainty

ISO 26000 says SR is “People and organizations behaving and conducting business ethically and with sensitivity toward social, cultural, economic, and environmental issues.” “The aim of SR is to contribute to sustainable development and the welfare of society.” I wonder why development is first and welfare is second??? Core issues: organizational governance, human rights, labor practices, the environment, fair operating practices, consumer issues, and contribution to community and society.

Environment, Social, and Governance conscious investors associate ESG with “sustainability;” a fuzzy, vaguely reliability related to: quality, durability, dependability, readiness, asset management, reliability growth, etc.. “The IFRS Foundation (International Financial Reporting Standards) created the International Sustainability Standards Board, which will function alongside and connect to the board that sets international accounting standards,…to provide investor-focused sustainability disclosure efforts.” [David Blood, in “How to Invest,…”by David Rubenstein] I wonder whether IFRS work will result in field reliability disclosure. 

ESG seems concerned with disclosure. Do warranty conditions and reliability disclosures conform to ESG disclosure requirements? Reliability disclosure seems part of sustainability disclosure and certainly part of resilience?

The San Francisco Bay Bridge Eastern truss span lasted from 1936 until the 1989 earthquake. The new, replacement span was plagued with steel anchor-rod corrosion due to inadequate protection. Every week in his “Weekly Update,” Fred Schenkleberg advocates “stay resilient. First you must make your products, processes, and services resilient. Efficiency is not worthwhile if products, parts, or processes are not resilient; i.e., if efficiency incurs unreliability of products or their supply chains. Imagine what would happen to a highly efficient, highly stressed, optimally designed series product, system, or process if one efficient part fails or deteriorates. Resilience requires more serious, statistical analysis than MTBF prediction with constant failure rates or Weibull analyses of a series system of independent components.

I programmed the maximum likelihood and least-squares nonparametric reliability estimators from ships and returns counts (from revenue and cost data required by GAAP) and the bootstrap forecast standard deviations in table 1. If you want reliability-based actuarial forecasts and their standard deviations, send ships and returns data to pstlarry@yahoo.com. 

References

Matthew D. Adler “Harsanyi 2.0,” SSRN Electronic Journal, Aug. 2011

Steven J. Brams, Michael A. Jones, and Christian Klamler, “Better Ways to Cut a Cake,” Notices of the AMS, Volume 53, Number 11, pp. 1314-1321, Dec. 2006

Carole Bernard, Christoph M. Rheinberger, and Nicolas Treich, “Catastrophe Aversion and Risk Equity in an Interdependent World,” Management Science, Vol. 64, no. 10, pp. 4490-4504, 2017

Peter S. Buczkowski, “Managing Warranties: Funding a Warranty Reserve and Outsourcing Prioritized Warranty Repairs,” PhD thesis, Univ. of North Carolina, Chapel Hill, 2004 (Everything you’ve ever wanted to know about warranty reserves, except that failures and repairs per unit are assumed to occur at a constant rate independent of age. Sales are random. Warranty costs are random.)

Coleman, Thomas, “A Practical Guide to Risk Management (A Summary),” Research Foundation of CFA Institute Monograph, https://ssrn.com/abstract=2279377, September, 2012

John C. Harsanyi, “Cardinal Welfare, Individualistic Ethics, and Interpersonal Comparisons of Utility,” Journal of Political Economy, vol. 63, pp. 309-321, 1955.

Ralph L. Keeney “Equity and Public Risk.” Operations Research, Vol. 28, no. 3, pp. 527-34, 1980

Ralph L. Keeney and Howard Raiffa, Decisions with Multiple Objectives: Preferences and Value Tradeoffs, Wiley, New York, 1976

Amy I. Kinkaid, CPA, J.D., MT, and Charles E. Federanich, “The Sec. 461 All-Events Test: Timing for Deducting Accrued Warranty Claims,” https://www.thetaxadviser.com/issues/2015/dec/sec-461-all-events-test.html#:~:text=A%20company%27s%20liability%20for%20warranties%20provided%20to%20its,all%20facts%20have%20occurred%20that%20establish%20the%20liability/December 1, 2015

V. G. Kulkarni, Shau-Shiang Ja, and Peter Buczkowski, “Managing Warranties and Warranty Reserves,” based on Buczkowski thesis. I can’t fine citation.

CFI Team, “Warranty Expense,” https://corporatefinanceinstitute.com/resources/accounting/warranty-expense/, 2022

W. Rick Viscusi, “Risk Equity,” Journal of Legal Studies, Vol. XXIX, June 2000

Daniel Cohen, Masako Darrough, Rong Huang, and Tzachi Zach, “Warranty Reserve: Contingent Liability, Informational Signal, or Earnings Management Tool?” 2008

Biserka Runje, Amalija Horvatić Novak, Andrej Razumić, Petar Piljek, Branko Štrbac, and Marko Orošnjak, “Evaluation of Consumer and Producer Risk in Conformity Assessment Decisions,” 30TH DAAAM International Symposium on Intelligent Manufacturing and Automation, pp. 54-58, 2019

Daniela Rroshi and Michael Weichselbaumer, “Reduction of Information Asymmetry: Evidence on the Role of a Consumer Association,” SSRN-id3796993.pdf, June 2022 

Bibliography on Warranty Cost and Warranty Reserves

Huai-qing Wu and William Q. Meeker, “Early Detection of reliability problems using information from warranty databases,” MMR 2002, www.math.ntnu.no. (Assumes the warranty db contains ages at failures and survivors’ ages by serial numbers, without errors.)

Lawless, Jerry, Joan Hu, and Jin Cao, “Methods for the estimation of failure distributions and rates from automobile warranty data,” Lifetime Data Analysis,” Vol. 1, pp. 227-240, 1995. (Accounts for mileage and age warranty limit. Same limitation as Wu and Meeker article. I did the same thing from aftermarket data: part sales, vehicle gozintos, and vehicle registration counts in neighborhoods of parts stores.)

Murthy, D. N. P., B. P. Iskandar, and R. J. Wilson, “Two-dimensional failure-free warranty policies: two-dimensional point process models,” Ops. Res., Vol. 43, No. 2, pp. 356-366, 1995 

Rao, B. M., “Algorithms for the free replacement warranty with phase-type lifetime distribution,” IIE Transactions, Vol. 27, pp. 348-357, 1995

Tapiero, Charles S. and Morton J. Posner, “Warranty Reserving,” Nav. Research. Logistics, Vol. 35, pp. 473-479, 1988. (Sales at fixed rate and price. Reserve is a fraction of revenue. Compound Poisson model assumed for warranty claims.)

Menke, Warren W., “Determination of Warranty Reserves,” Man. Sci., Vol. 15, No. 10, pp. B-542-B-549June 1969. (Nonrepairable products. Failures per product are assumed to occur at a constant rate independent of age.)

Kaminskiy, Mark P. and Vasiliy V. Krivtsov, “ G-Renewal process as a model for statistical warranty claim prediction,” RAMS Proceedings, pp. 276-279, 2000. (Introduces hysteresis model for the extent to which repair restores age: good-as-new, good-as-old, or somewhere in between.)

Monga, Amit, and Ming J. Zuo, “Optimal system design considering maintenance and warranty,” Computers Ops. Res., Vol. 25, No. 9, pp. 691-705, 1998. (Life cycle cost model including everything but the kitchen sink. Optimized by genetic algorithm.) 

Zaino, Nicholas and Toby Berke, “Some renewal theory results with application to fleet warranties,” Nav. Res. Logistics, Vol. 41, pp. 465-482, 1994. (By “fleet warranty,” the authors refer to a supplier who guarantees that the product mean life will be at least some specified value. If it doesn’t, customer is compensated proportional to number of observed failures.)

J. D. Kalbfleisch and J. F. Lawless, “Methods for the analysis and prediction of warranty claims,” TR STAT-89-31, U. of Waterloo

F. M. Biedenweg, “Warranty policies: consumer value vs. manufacturer cost,” Stanford University dissertation, 1981

T. S. Glickman and P. D. Berger, “Optimal price and protection period: decisions for a product under warranty,” Man. Sci. Vol. 22, No. 12 Aug 1976

U. Karmarkar, “Future costs of service contracts for consumer durable goods,” AIIE Trans, Vol. 10, No. 4, 1978

D. G. Nguyen and D. N. P. Murthy, “A general model for estimating warranty costs for repairable products,” IIE Trans,Vol. 16, No. 4. Dec. 1984

W. R. Blischke and E. M. Scheuer, “Applications of renewal theory in analysis of the free replacement warranty,” Nav. Res. Log. Quart., Vol. 28, No. 2, 1981

K. R. Balachandran et al, “Product warranty period: a Markovian approach…,” The Accounting Review, Vol. LVI, No. 1, 1981

M. U. Thomas, “Optimum warranty policies for nonrepairable items,” IEEE Trans. on Rel., Vol. R32, No. 3, 1983

P. R. Ritchken and C. S. Tapiero, “Warranty design under buyer and seller risk aversion,” Nav. Res. Log. Quart., Vol. 33, 1986

W. R. Blischke and E. M. Scheuer, “Calculation of the cost of warranty policies as a function of estimated life distribution,” Nav. Res. Log. Quart., Vol. 22, No 4, 1975

J. W. Mamer, “Cost analysis of pro rata and free replacement warranties,” Nav. Res. Log. Quart., Vol. 29, No 2, 1982

D. G. Nguyen and D. N. P. Murthy, “Cost analysis of warranty policies,” Nav. Res. Log. Quart., Vol. 31, 1984

E. E. Anderson, “Product price and warranty terms: an optimization model,” Opl. Res. Q., Vol. 28, No. 3, 1977 

D. G. Nguyen and D. N. P. Murthy, “Failure free warranty policies for nonrepairable products: a review and some extensions,” Recherche Operationnelle, Vol. 22, No 2, 1988 

J. P. Keating and R. C. Magel, “Comments on estimators based on error in the predicted distribution function,” Commun. Statist. Theor. Meth., Vol. 13, No 15, 1984

V. L. Hill and W. R. Blischke, “An assessment of alternative models in warranty analysis,” J. Inf. and Opt. Sciences,Vol. 8, 1987

D. G. Nguyen and D. N. P. Murthy, “An optimal repair cost limit policy for servicing warranty,” Mathl. Comput. Modelling, Vol. 11, 1988

Y. Balcer and I. Sahin, “Replacement costs under warranty: cost moments and time variability,” Ops. Res., Vol. 34, No. 4, 1986

J. Mamer, “Discounted and per unit costs of product warranty,” Man. Sci., Vol. 33, No. 7, 1987

K. Bosch, “Garantie-und Lulanzstrategien,” OR Spectrum, Vol. 29, No. 7, 1985