
Making the Right Choice in Reliability Engineering
In reliability engineering, we often need to extrapolate test data collected under accelerated stress conditions to predict performance under normal operating conditions. Two mathematical models commonly used for this purpose are the power-law model and the exponential model. But which one should you choose when your data fits both models equally well? This article explores the differences between these models and provides practical guidance on making this critical decision.
/more
Understanding Acceleration Factor ModelsAcceleration factor (AF) models allow us to relate the Time-to-Failure (TF) under accelerated test conditions to the expected lifetime under normal operating conditions. These models are essential for predicting product reliability without waiting for failures to occur under normal use conditions.The two primary models are:
- Power-law model: TF = A × S^(-n) Where S is the stress level, A is a constant, and n is the power-law exponentExponential model: TF = B × exp(-C×S) Where S is the stress level, B is a constant, and C is the exponential coefficient
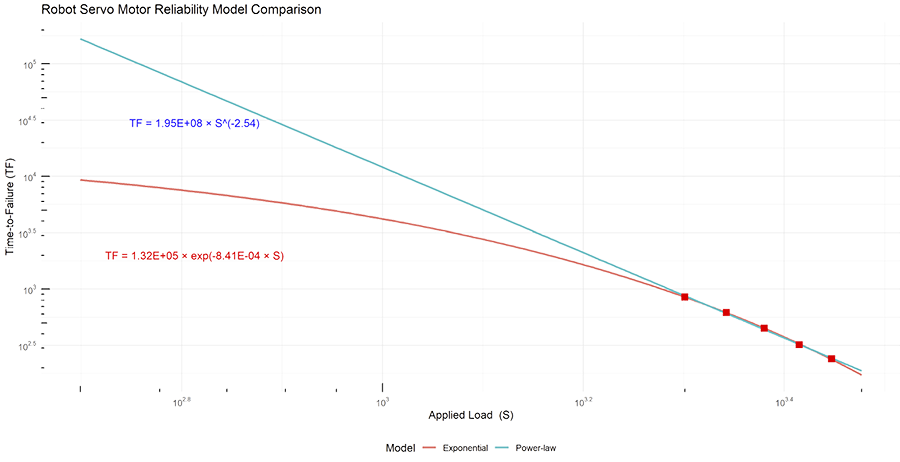
Both models can often fit the same accelerated test data with similar statistical goodness of fit, yet they may predict dramatically different lifetimes when extrapolated to lower stress levels.The Conservative Approach: When Both Models FitWhen faced with data that can be reasonably fitted by either model, reliability engineers should consider a fundamental principle: choose the model that provides the more conservative prediction.Based on extensive empirical evidence, including the example shown in the image, the exponential model typically produces:
- Smaller TF (Time-to-Failure) valuesSmaller AF (Acceleration Factor) values
When extrapolating from stress conditions to use conditions, these smaller values represent a more conservative approach. This is why the exponential model is often referred to as the “conservative model” in reliability engineering.
Physics of Failure Considerations
While the conservative approach is generally advisable, understanding the underlying physics of failure can provide additional insights for model selection:
- If there’s a clear physical mechanism that supports one model over the other, that model should be preferred
- Different failure mechanisms may be better represented by different models
- Temperature or stress thresholds may exist where the dominant failure mechanism changes
For example, in a servo motor with integrated planetary gearbox, the failure mechanism transitions from mechanical fatigue at normal temperatures (with activation energy Q_fatigue) to lubricant oxidation at higher temperatures (with activation energy Q_oxidation, where Q_oxidation > Q_fatigue). This shift in failure physics significantly impacts model selection—power-law models may better represent mechanical wear at normal temperatures, while exponential models better capture the accelerated chemical degradation of lubricants at elevated temperatures.
A Practical Example: Visualizing the Difference
Let’s examine a practical example from robotics: accelerated testing of bearings in a servo motor used in industrial robots. Engineers need to predict bearing life under normal operation but can only collect data under accelerated conditions using increased loads. When no information about the failure mechanisms (or PoF) is know fitting both the models to the same TF data shows good fit. However, the values are significantly different when prediction at lower use-case stress is done.
Conclusion
When choosing between power-law and exponential models that fit your accelerated test data equally well:
- Default to the conservative approach: Use the exponential model for more conservative predictions unless there’s compelling evidence to do otherwise.
- Consider physics of failure: If you have a solid understanding of the underlying failure mechanisms, use this knowledge to guide your model selection.
- Perform sensitivity analysis: Evaluate how model selection affects your reliability predictions and risk assessments.
- Document assumptions: Clearly articulate your rationale for model selection in reliability reports and assessments.
By following these guidelines, reliability engineers can make more informed decisions about acceleration models, leading to more reliable products and systems.
What has been your experience with acceleration factor models? Have you encountered situations where model selection significantly impacted your reliability predictions? Share your thoughts in the comments below.



